Clearing financial networks: Impact on equilibrium asset prices and seniority of claims

In financial derivatives networks, clearinghouses have been mandated as de facto central nodes: they are buyers to the sellers of financial contracts and resellers to the ultimate buyers. Other services such as portfolio compression aim at solving various network problems such as reducing cycles. All these services face complex challenges, ranging from the direct effect on the network topology to the indirect effects on asset prices and on the end users. In our research, we raise two main points that have received less attention in the literature. Firstly, an equilibrium price for the asset prices may not be achieved in a general payment network, but, in general, higher asset prices are achieved after using central clearing or portfolio compression services. Secondly, portfolio compression and clearinghouses modify the seniority structure in the network, and end users that are not part of multilateral clearing arrangements may become de facto junior.

In the decade since the financial crisis, there has been an extraordinary effort in the academic community to study counterparty risk at the level of the financial system (rather than in isolation, as was the case before the crisis). Systemic risk emerged as an important concept and network science became a predominant tool to study it, i.e., to understand what happens at system level when a shock is propagated through a variety of interconnections. The framework introduced by Larry Eisenberg and Thomas H. Noe has proven particularly versatile, and many researchers incorporated various channels through which risk spreads in financial networks. The prevailing notion of equilibrium is very intuitive: a node is either able to pay in full what it owes to others or it will pay proportionally all its receivables. Its receivables in turn depend on what everyone else will pay to it. The payment or clearing equilibrium is precisely the network fixed point.

Without central counterparty clearinghouses, each party of a contract has the risk that the other party cannot pay. When we introduce a CCP, it becomes a central node in the complex network of OTC financial derivatives. Because counterparty risk is transferred to the CCP, the CCP also receives from the member institutions capital in various forms to bear any potential losses. When novation happens at the level of a network of contracts, the network becomes a star network and multilateral netting occurs. Each node will pay its net payable of the original network, namely the difference between its total payables and its total receivables. The gross payables are vastly reduced. A CCP not only reduces gross payables, it also reduces the length of contract chains. Portfolio compression is another way to modify the network of payables. Several parties in the network enter into a multilateral agreement to essentially reduce the cycles in the network.

In our work we show that the Eisenberg-Noe framework can be used to assess the effect of clearinghouses and portfolio compression on the end users and on asset prices. Contingent claims can have an impact on asset prices, which depend on the network structure of the liabilities. We find that centralised clearing as well as portfolio compression, which keeps net liabilities constant while removing cycles, both increase asset prices and consequently the aggregate surplus. However, both these techniques can have unintended consequences on end users or other parts of the network that are left outside multilateral netting agreements. End users and non-clearing members may become junior whereas clearing members become senior.

Consider the case where in the initial network there are end users who are senior to the banks across the network. Systemic risk can be defined as the shortfall on the end users, in other words on the economy at large. If one centrally clears the interbank liabilities, the end users become de facto junior with respect to the nodes in the netted system. Indeed, for every node whose liabilities are cleared by the CCP, the non-cleared liabilities are junior. To the extent to which more resources of these nodes are reserved to the netted network, the outside users are bearing more of the loss.

To see this, consider the following simple example in Figure 1. For each node we write in brackets its cash holdings, if any. On the edges we write how much of the total payables is paid in the Eisenberg-Noe equilibrium: for example 40/50 denotes that the node is able to pay in equilibrium $40 out of $50. In the case without clearing, since the end users are senior they will receive their liability in full: in equilibrium, node 2 (which holds $60 in cash) pays $100 to node 3. Out of this $100, node 3 will pay the end users first, and therefore they will receive $60 in full. With a CCP, node 2 will pay $50 (its net liability) now to the CCP and the CCP will distribute this to nodes 1 and 3 in proportion to their net receivables. Instead of $100 as in the previous case, node 3 now has $30 which will be passed to the end users. The outcome with the CCP is the same outcome as without CCP but in which the cycle is de facto senior to the liability to the end users, quite the opposite of the initial situation.

Portfolio compression means that a cycle in the network is removed: all liabilities on the cycle are decreased by the smallest liability (and consequently that smallest liability disappears, thus breaking the cycle). In the previous example, if there is portfolio compression on the cycle, the end users will benefit with respect to the centrally cleared

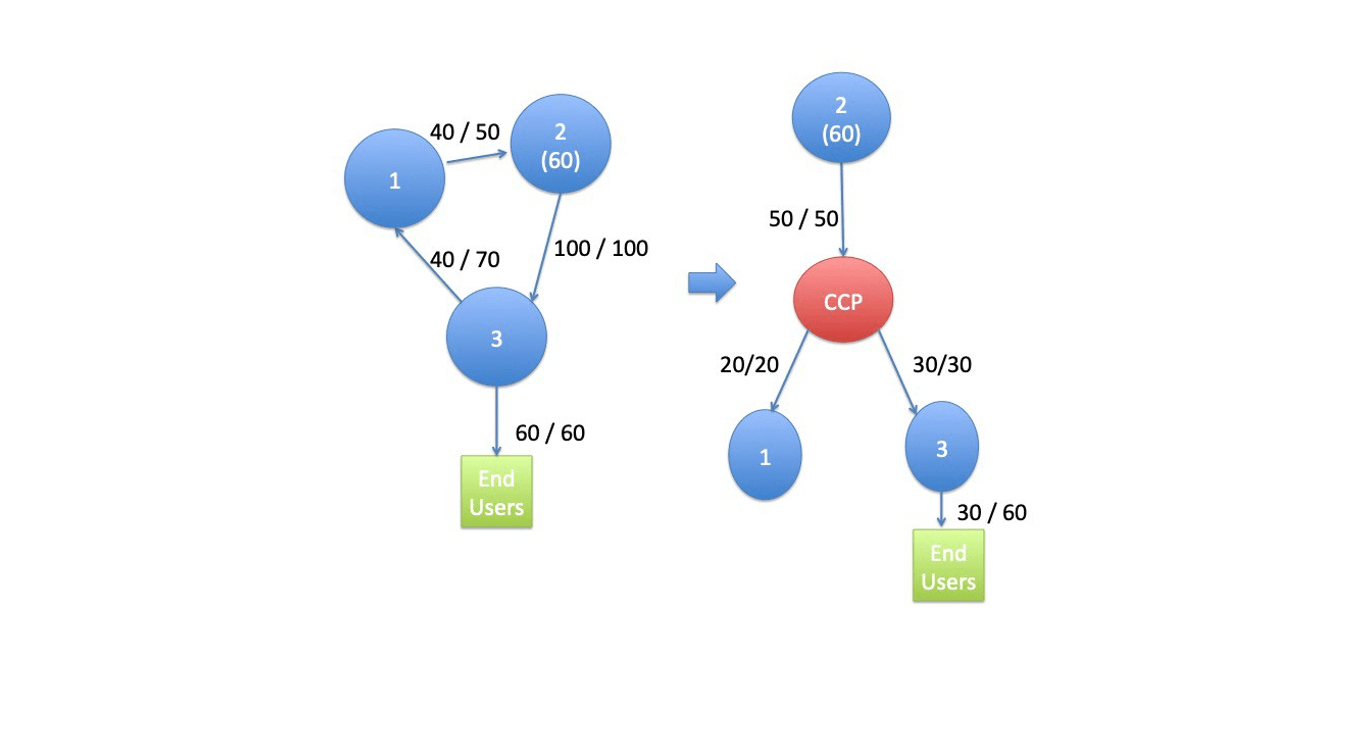
Figure 1: Equilibrium payments. Centrally clearing changes the seniority structure and can increase systemic risk.

case, but they will still be worse than in the non-cleared case; see Figure 2. This shows that portfolio compression can be better for end users than centralised clearing.

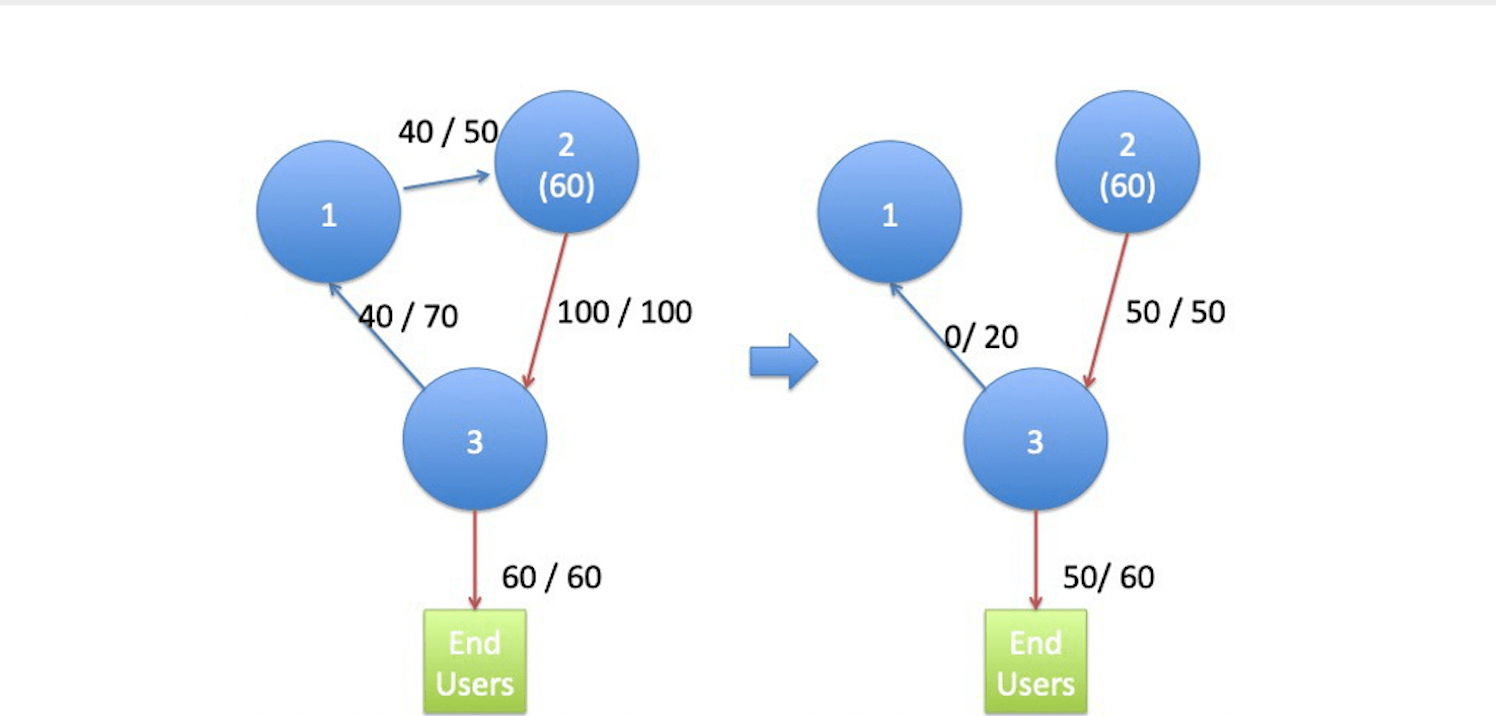
Figure 2: The red path is a seniority path. Under portfolio compression end users may benefit with respect to the centrally cleared case, when they are not included in the central clearinghouse.

If CCP and portfolio compression services could be brought to all parts of the financial network, then the risk in seniority loss would all but disappear. However, as institutions pose different counterparty risk, a tradeoff is present and it may not be optimal from the point of view of counterparty risk that all institutions participate. The recent development of blockchain and smart contract technology brings the potential of decentralisation of multilateral netting and portfolio compression. The idea is that instead of one central counterparty managing the risk-bearing capital, smart contracts could lock in collateral against the risk in the financial contracts. We expect that more collateral would be necessary than in traditional systems. Designing blockchains that could incorporate multilateral netting remains an open problem, and the main challenge ahead lies in designing a decentralised clearing system which strikes the optimal balance between excessive collateralisation and counterparty risk.

Forthcoming in TutORials in Operations Research